2017-12-31

2017年を振り返る

このブログにしては珍しくこの1年を振り返ります。

以下の記事での補足を年内にやります！って言いましたが忙しくてやれず・・・。楽しみにしていた方々申し訳ありません。。。 lyricalmaestrojp.hatenablog.com

その代わり、今回の記事を見て、こんなことがあったなー、ぐらいに見ていただければ幸いです。

2017-12-13

関数解析復習会のその先「Weyl-von Neumannの定理」

数学カフェAdvent Calender 12/13分です。

adventar.org

前回の記事に引き続き今回も関数解析関連のトピックです。

lyricalmaestrojp.hatenablog.com

今回はWeyl-von Neumannの定理について紹介します。

Thm (Weyl-von Neumann)

可分な無限次元Hilbert空間 $\mathscr{H}$ 上の有界自己共役作用素 $H$ と正の数 $\epsilon \gt 0$ に対して、 $$ H = D + K , \ \ \ \ \ \Vert K \Vert \lt \epsilon $$ となる有界自己共役対角作用素 $D$ とCompact作用素 $K$ が存在する。

関数解析復習会でCompact作用素とFredholm作用素について取り扱っていたので、これらの考えを応用させた定理を紹介してもいいのでは？というのでこの定理の紹介をすることにしました。

前提知識は関数解析復習会でやった内容(黒田の関数解析)と前回の私のブログの記事でしょうか。

参考文献等はこの記事の後半で紹介します。

2017-12-11

掛け算作用素でCompact作用素・Fredholm作用素の理論を展開する

数学カフェ Advent Calendar 12/11分の記事です。

1. はじめに

みなさま、こんばんは。まえすとろ(@maestro_L_jp)です！僕は学生の頃数学科で数学の勉強をしていました。その中で大学院では作用素環論を専攻していました。作用素環論は「Hilbert空間上の有界線型作用素たちから構成される環の構造について調べる理論」です。この分野について勉強するために関数解析の必須の知識となります。なので、ある程度の知識は有していたりします。そして、数学カフェで何回かに渡り、関数解析の予習会+復習会が開催され私もそのうち何回か参加させていただきました。そこでCompact作用素とFredholm作用素についてのトピックを扱っていたので、これを使った題材で書こう！と思った次第です。とはいえ、今は(昔からだったかもですが)最先端の内容を話すことできないので、Compact作用素、Fredholm作用素の議論を、掛け算作用素でやったらどうなるか、ということについて書いていこうかと思います。自分はこの掛け算作用素に帰着して一般的な作用素の議論を理解してきました。関数解析で作用素論とか勉強する人にとって中身をしっかり味わうための触媒的なものになれば幸いです。

ここから口調が数学のテキストっぽくなります。あと、第3章以降の命題・定理の証明は以下のpdfファイルにまとめてあります。ちょっと乱調気味ですがご了承ください。 https://drive.google.com/open?id=1mVHh0MzljqHZdNq7Nz2Iq2WWt5SFqJOO

なお、今回は話を簡単にするためBanach空間でなく同一のHilbert空間上の線型作用素に限定してお話しさせていただきます。

2. 今回取り扱う概念の定義と命題・定理

Def 2.1. Hilbert空間 $\mathscr{H}$ から $\mathscr{K}$ への線型作用素 $T$ が以下の条件を満たす時、 $T$ は有界である(有界線型作用素 or 連続線型作用素)と定義する。

$$ {}^\exists M > 0 \ \ \ s.t. \ \ \ {}^\forall x \in \mathscr{H} \ \ \ \Vert Tx \Vert \leq \Vert x \Vert $$

このとき、 $T$ のノルムを $\displaystyle \Vert T \Vert \equiv \sup_{ \Vert x \Vert = 1 } \Vert Tx \Vert$ と定める。また、 $\mathscr{H}$ から $\mathscr{H}$ への線型作用素を $\mathscr{H}$ 上の線型作用素 という。

Prop 2.2. Hilbert空間 $\mathscr{H}$ から $\mathscr{K}$ への線型作用素 $T$ について以下は同値。

(1) $T$ は有界である。

(2) $\displaystyle \lbrace x_n \rbrace_n$ が $\mathscr{H}$ の収束列ならば、 $\displaystyle \lbrace Tx_n \rbrace_n$ は $\mathscr{K}$ の収束列で、 $\displaystyle \lim_{ n \to \infty } Tx_n = Ty$ が成り立つ。

(ただし、 $\displaystyle \lim_{n \to \infty} x_n = y$ 。)

Def 2.3. Hilbert空間 $\mathscr{H}$ から $\mathscr{K}$ への線型作用素 $T$ が以下の条件を満たすとき、 $T$ はCompact作用素である(あるいは完全連続線型作用素)と定義する。

$\displaystyle {}^\forall \lbrace x_n \rbrace_n : \mathscr{H} の有界点列 \ {}^\exists \lbrace x_{n(k)} \rbrace_k : \lbrace x_n \rbrace_n の部分列 \ \ \ s.t. \ \ \ \lbrace Tx_{n(k)} \rbrace_k は \mathscr{K} の収束列$

Prop 2.4. Compact作用素は有界線型作用素である。

Def 2.5. Hilbert空間 $\mathscr{H}$ 上の有界線型作用素 $T$ について、以下の条件を満たす有界線型作用素 $T^*$ を $T$ の共役作用素という。

$$ \langle T^* x, y \rangle = \langle x, Ty \rangle \ \ ( {}^\forall x, y \in \mathscr{H})$$

特に、 $T^*=T$ が成り立つ時、 $T$ を自己共役作用素という。

Prop 2.6. 有界線型作用素 $T$ に対する共役作用素 $T^*$ は一意に存在する。

Def 2.7. Hilbert空間 $\mathscr{H}$ 上の有界線型作用素 $T$ が以下の3つの条件を満たす時、 $T$ はFredholm作用素であると定義する。

(1) $\mathrm{ Ker} T$ は有限次元。

(2) $\mathrm{ Ker} T^*$ は有限次元。

(3) $\mathrm{ Range} T$ は $\mathscr{H}$ の閉部分空間。

Prop 2.8. 有界線型作用素 $T$ がFredholm作用素である必要十分条件は、 $$ ST = I - K, \ \ \ TS' = I - K'$$

となる有界線型作用素 $S, S'$ とCompact作用素 $K, K'$ が存在することである。(ただし、 $I$ は恒等作用素である。以後、 $I$ は恒等作用素とする)

Def 2.9.

(1) 複素数 $\lambda$ が有界線型作用素 $\lambda I - T$ についてが可逆な有界線型作用素を持つ時、 $\lambda$ は有界線型作用素 $T$ のレゾルベントという。 $T$ のレゾルベント全体の集合を $\rho( T )$ と書く。

(2) $\mathbb{ C } \setminus \rho( T )$ を $T$ のスペクトル集合といい $\sigma (T)$ と書く。 $\sigma (T)$ の元を $T$ のスペクトルという。

(3) $T$ のスペクトル $\lambda$ について、 $( \lambda I - T) x = 0$ となる非ゼロのベクトル $x$ が存在する時、この $\lambda$ を点スペクトル(いわゆる固有値)といい、点スペクトル全体の集合を $\sigma _{\mathrm{ p} } (T)$ と書く。 $\mathrm{Ker}( \lambda I - T)$ をスペクトル $\lambda$ に対する固有空間という。

(4) $T$ のスペクトル $\lambda$ について、 $( \lambda I - T)$ は単射かつ $\mathrm{Range}( \lambda I - T)$ は $\mathscr{H}$ の中で稠密だが、 $( \lambda I - T) ^{-1}$ は有界でない場合、この $\lambda$ を連続スペクトルといい、連続スペクトル全体の集合を $\sigma _{\mathrm{ c} } (T)$ と書く。

Thm 2.10. (Fredholm Alternative)

Compact作用素 $T$ について以下のどちらかが必ず成り立つ。

$I - T$ は可逆な有界線型作用素を持つ。
$\displaystyle \mathrm{Ker}(I - T) \neq \lbrace 0 \rbrace$ でかつ有限次元。

Prop 2.11. (Compact作用素のスペクトル)

・Compact作用素のスペクトル集合は0以外の集積点を持たない。

・Compact作用素のスペクトル $\lambda ( \neq 0)$ について、 $\lambda$ の固有空間は有限次元。

Def 2.12.

複素数 $\lambda$ が有界線型作用素 $T$ について、 $\lambda I - T$ がFredholm作用素にならない時、 $\lambda$ は有界線型作用素 $T$ の本質的スペクトルといい、本質的スペクトル全体の集合を $\sigma _{\mathrm{ess} } (T)$ と書く。

有界線型作用素はどんなものかはイメージしやすいが、Compact作用素やFredholm作用素、上記の命題・定理などは初学者にとってはイメージしづらいものである。次の章で「数列空間上の掛け算作用素」をベースにした議論を行い本章で紹介した定義・命題・定理などを理解しやすい形に昇華していく。

3. 掛け算作用素についての基本的な性質

以下、Hilbert空間として複素数列空間 $\displaystyle l^{2} = \lbrace \lbrace x_n \rbrace_n \ \mid \ \sum_{n = 1}^{\infty} |x_n|^{2} \lt \infty \rbrace$ を取り扱う。

Prop 3.1. $\displaystyle c := \lbrace c_n \rbrace_n$ を $\displaystyle l^{\infty} (:= \lbrace \lbrace x_n \rbrace_n \ \mid \ \sup_n |x_n| \lt \infty \rbrace)$ 上に属する複素数列とする。

線型作用素 $M_c$ を

$$ M_c x := \lbrace c_n x_n \rbrace_n \ \ \ \ ( x \in l^{2})$$

とすると、 $M_c$ は有界線型作用素である。

この $M_c$ を掛け算作用素という。

以下、掛け算作用素の基本的な性質を紹介する。

Prop 3.2. (掛け算作用素の和・スカラー倍・積)

$c, d \in l^{\infty}, \alpha \in \mathbb{ C }$ について、以下が成り立つ。

(1) $M_c + M_d = M_{c+d}$

(2) $\alpha M_c = M_{\alpha c}$

(3) $M_c M_d = M_{cd}$

Prop 3.3. (掛け算作用素の共役作用素)

$\displaystyle c = \lbrace c_n \rbrace_n \in l^{\infty}$ について、 $M_c$ の共役作用素は $M_{\bar{ c } }$ である。ただし、 $\displaystyle \bar{ c } := \lbrace \bar{ c_n } \rbrace_n$ である。

Prop 3.4. 掛け算作用素 $M_c$ が自己共役作用素であるための必要十分条件は $c$ が実数列であることである。

4. 掛け算作用素上でのCompact作用素・Fredholm作用素の理論

まず、掛け算作用素がCompact作用素になる条件を条件を与える。これをベースにCompact作用素、Fredholm作用素にまつわる諸定理との関連を述べる。

Prop. 4.1.

掛け算作用素 $M_c$ がCompact作用素になる必要十分条件は $\displaystyle c = \lbrace c_n \rbrace_n$ が0に収束する数列になることである。

この命題から言えることは、Compact掛け算作用素を取り扱う際、0に収束する数列をイメージしていけばOKということになる。(ここから得られた知見は、掛け算作用とは限らないCompact作用素について取り扱う時の道しるべになったりする) 数列は横軸にindex, 縦軸に項の値をとる座標を考えると、実数列 $\displaystyle c = \lbrace c_n \rbrace_n$ の絶対値は図にプロットできる(図1)。

f:id:maestro_L_jp:20171210234343p:plain

これだけでも数列の振る舞いはわかる。プロットした点を結ぶようにグラフを書くと、nを十分大きくしていったときの振る舞いがわかりやすくなる(図2)。

f:id:maestro_L_jp:20171210234410j:plain

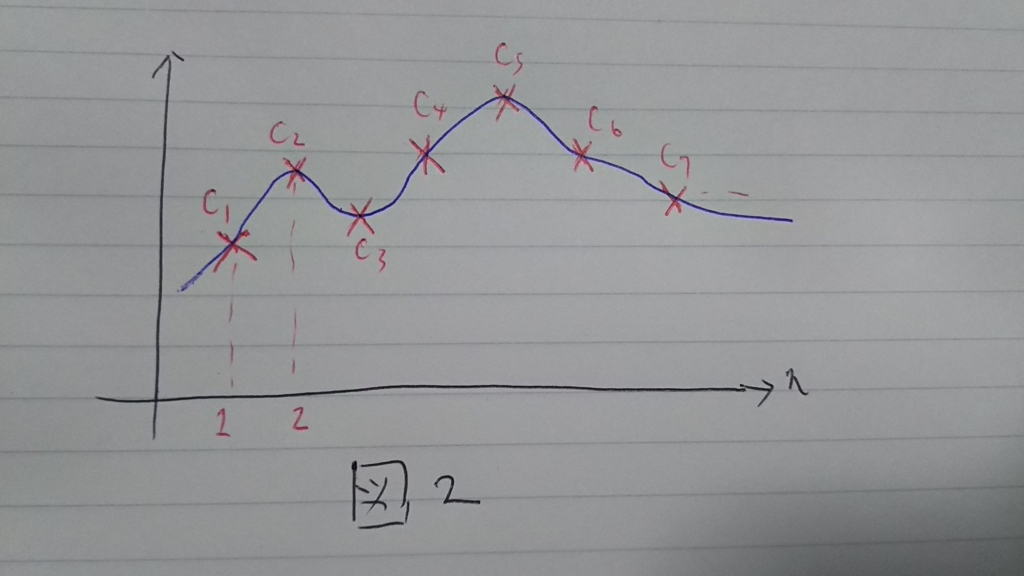
Compact自己共役掛け算作用素 $M_c$ に対応する収束列 $\displaystyle c = \lbrace c_n \rbrace_n$ は以下のように図示できる(図3)。

f:id:maestro_L_jp:20171210234646j:plain

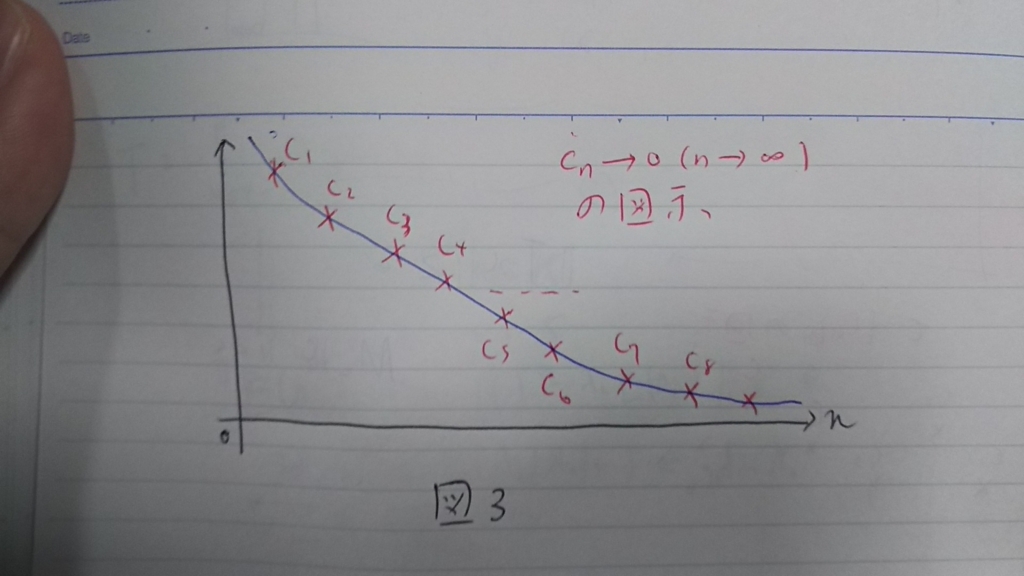
ここで、作用素 $I - M_c$ を考える。この作用素は掛け算作用素になり対応する数列 $d$ は $\displaystyle \lbrace 1 - c_n \rbrace_n$ となる。 $M_c$ がCompact作用素なら、 $\displaystyle \lbrace c_n \rbrace_n$ は0への収束になるので、 $d$ は1への収束列になる。図4に $d$ を図示したものを表示させる。

f:id:maestro_L_jp:20171210235124p:plain

この図から見えてくるのは、「nが十分大きくした場合、数列の値は「1」との距離が0.5以下になる」ということである。 $M_c$ が可逆かどうかはindexが若い有限個の項だけみていいだろうとあたりがつく。このことは以下に定理としてあげる。

Thm 4.2. (掛け算作用素版Fredholm Alternative) Compact掛け算作用素 $M_c$ について以下のどちらかが必ず成り立つ。

$I - M_c$ は可逆な有界線型作用素を持つ。(数列 $\displaystyle \lbrace 1 - c_n \rbrace_n$ は0に値をとることはない)
$\displaystyle \mathrm{Ker}(I - M_c) \neq \lbrace 0 \rbrace$ でかつ有限次元。(数列 $\displaystyle \lbrace 1 - c_n \rbrace_n$ で、0に値を取る項は高々有限個存在する。)

掛け算作用素がFredholm作用素になる条件を条件を与える
Prop.4.3. 掛け算作用素がFredholm作用素である必要十分条件は、以下の2つを満たすことである。

(1) 対応する数列の集積点に0を含まないことである。

(2) 対応する数列の中で0に値をとる項は高々有限個。

自己共役掛け算作用素に対応する数列について以下に図示する。Fredholm作用素である例とそうでないものの例を図示する(図5)。

f:id:maestro_L_jp:20171210235739p:plain

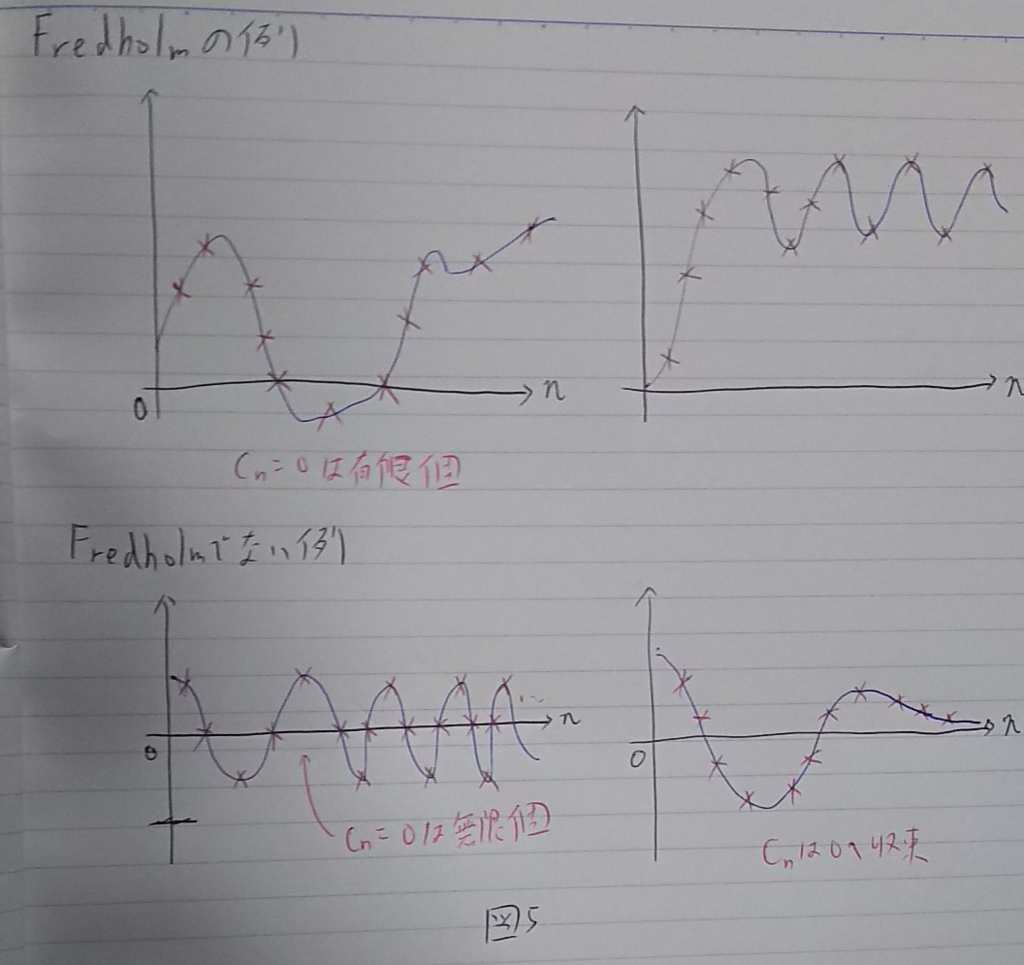
以下の命題はProp 2.8. の掛け算作用素版である。別資料に証明は記載するが、Fredholm掛け算作用素の場合は、点列ベースで考えていけば直感から外れることなく、かつ数学的に厳密な方法で証明できる。

Prop 4.4. 掛け算作用素 $M_c$ がFredholm作用素である必要十分条件は、 $$ M_d M_c = I - M_k, \ \ \ M_c M_{d'} = I - M_{k'}$$

となる $d, d' \in l^{\infty}$ と0への収束列 $k, k'$ が存在することである。

掛け算作用素のスペクトルについても議論する。

Prop 4.5.

掛け算作用素 $M_c$ のスペクトルについて以下が成り立つ。

$\sigma (M_c) = \overline{ \lbrace x_n \mid n = 1, 2, … \rbrace }$

$\sigma_{\mathrm{p} } (M_c) = \lbrace x_n \mid n = 1, 2, … \rbrace$

$\sigma_{\mathrm{c} } (M_c) = \sigma (M_c) \setminus \sigma_{\mathrm{p} } (M_c)$

が成り立つ。(補足すると $\sigma_{\mathrm{c} } (M_c)$ は数列のとる値の集積点の中で、実際に値を取る項が存在しない。)

Ex 4.6.

数列 $\displaystyle c = \lbrace \frac{n}{n+1} \rbrace_n$ に対応する掛け算作用素 $M_c$ については

$\sigma (M_c) = \lbrace \frac{n}{n+1} \mid n = 1, 2, … \rbrace \cup \lbrace 0 \rbrace$

$\sigma_{\mathrm{p} } (M_c) = \lbrace \frac{n}{n+1} \mid n = 1, 2, … \rbrace$

$\sigma_{\mathrm{c} } (M_c) = \lbrace 0 \rbrace$

となる。以下に数列 $c$ について図示する。以下の図で点スペクトルが実際数列の項がとる値、連続スペクトルが収束先になることも図示する(図7)。

f:id:maestro_L_jp:20171211000106p:plain

これは掛け算作用素のスペクトルについて調べるには数列のとる値を調べていけばいいということを主張している。

掛け算作用素については以下のことも言える。

Prop 4.7. 掛け算作用素におけるスペクトルの固有空間の次元はその値をとる数列の項の数である。

この事実とCompact掛け算作用素が0への収束列に対応することから、以下の定理が成り立つ。

Thm 4.8. (Compact掛け算作用素のスペクトルと固有空間)

・Compact掛け算作用素のスペクトル集合は0以外の集積点を持たない。

・Compact掛け算作用素のスペクトル $\lambda ( \neq 0)$ について、 $\lambda$ の固有空間は有限次元。

Prop 4.9. (掛け算作用素の本質的スペクトル)

掛け算作用素 $M_c$ の本質的スペクトルについて以下が成り立つ。

$\sigma_{\mathrm{ess}} (M_c) = \lbrace \lambda \in \mathbb{C} \mid \lambda = c_n となる nが無限個 \rbrace \cup \lbrace \lambda \in \mathbb{C} \mid \lambda は \lbrace c_n \mid n = 1, 2, … \rbrace の集積点 \rbrace$

自己共役掛け算作用素 $M_c$ に対応する実数列 $\lbrace c_n \rbrace_n$ を図示して本質的スペクトルがどういうものかイメージしやすいようにしておく(図8)。

f:id:maestro_L_jp:20171211000536p:plain

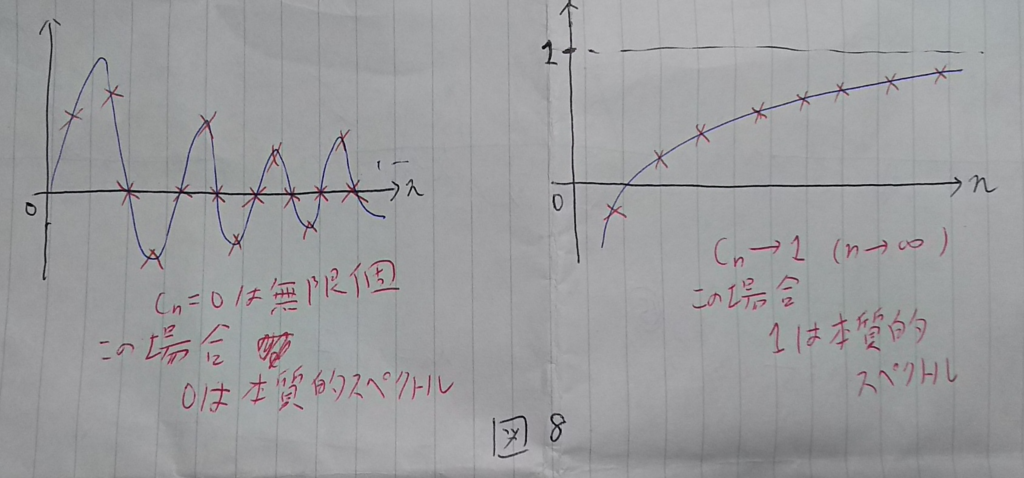
5. まとめ

いかがだったでしょうか。掛け算作用素ベースでCompact作用素やFredholm作用素を扱うと意外と敷居が低くイメージしやすいと思います。この帰着によって私は作用素論の理解を深めていきました(ただし、万人にこの方法で以下はまた別問題…)

特に一番このイメージが効いたのは以下の定理の証明を読み解いていくときである。(というか、修論もこのイメージがなければ書けなかった。。)

Thm 有界自己共役作用素 $T,S$ について以下の二つは同値。

(1) $\sigma_{\mathrm{ess}} (T) = \sigma_{\mathrm{ess}} (S)$

(2) 等式 $T - USU^* = K$ を満たすユニタリー作用素 $U$ とCompact作用素 $K$ が存在する。

この定理はWyle - von Neumann の定理の応用として、次のAdvent Calenderで証明していきます。

2017-11-23

【自主セミナー】ベイズ統計オンラインセミナー第3回

開催日付: 2017/11/11

今回やった内容の範囲: ThinkBayes 第2章

今回は友人に発表をお願いしました(なので友人が資料をアップしない限り、資料の共有はなし。)

今回は計算機統計ということでPython3ベースのコードを使ってベイズの問題を解くとどうなるか？というのをやりました。基本的にはPythonになれましょう！というのと、第1章で取り扱った内容を復習しましょうという感じでした。

M&M問題を解くときに出てきた、「ベイズ更新」的に表を二つ重ねていたところは面白かったと思います。ベイズ計算をまとめて１つにするケースと1つずつn回やるケースで条件が一緒なら答えは一致するというのもわかって面白かったです(プログラム的には後者のスタンスで書いてあったので)

f:id:maestro_L_jp:20171123173628p:plain

この章の最後に演習問題があるのだが…初めてPYthonの派生クラスのメソッド(オーバーライド先)からオーバーロード元のメソッドを呼ぶ方法を知りました。Python2と3でだいぶ違いましたが。。。

www.lifewithpython.com

次回(2018/1/8予定)は3章をやります。しかも！久々におふらいんでやります。オフラインでやる特典として数学色を強めに出していきます。

2017-11-11

【自主セミナー】ベイズ統計オンラインセミナー第2回

開催日付: 2017/11/11 今回やった内容の範囲: ThinkBayes 第1章

あ、いきなり書いていますが、これ、内輪でやっている自主セミナーの記録です。テキストはThinkBayesってやつ。

https://www.amazon.co.jp/Think-Bayes-%E2%80%95%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%9E%E3%81%AE%E3%81%9F%E3%82%81%E3%81%AE%E3%83%99%E3%82%A4%E3%82%BA%E7%B5%B1%E8%A8%88%E5%85%A5%E9%96%80-Allen-Downey/dp/4873116945

こちらが今回使ったセミナーの資料。

ベイズ統計セミナーVol2 from まえすとろ

www.slideshare.net

基本的にやったことは・Bayesの定理を元に問題を解く手順の紹介・実際手順通りにいくつかの問題を解く。といった感じのことでした。

なんとなくみなさん解くのに慣れていただいたみたいです(+自分でアレンジした方法の不備があったのでそれの修正も行うことができました。)

次回は2章、3章をやります。

2017-10-02

【第21回数学カフェ】蔵本モデルと一般化スペクトル理論に参加してきました。

9/23(土)に開催された【第21回数学カフェ】蔵本モデルと一般化スペクトル理論に参加してきました。

connpass.com

会場はオラクルJapan青山オフィス。前回の超越数論の回でもお世話になった場所です。今回の発表でもホワイトボードをメインに使った議論をしていたのですが、前回ここで数学カフェやった時と違ったのがスクリーンに写っているスライドが存分に力を発揮していたことでしょうか。

今回の講師は九州大学の千葉先生。同期現象を起点にいろいろ話を進めていってくれたので最後の章部分以外はなんとか十二分に理解できてたと思います。参考文献等は上記のconnpassのサイトに書いてありますのでそちらをご参照ください。

1. 蔵本モデルとは?

まず、同期現象とはなにかをホタルの光などをたとえに説明されていました。そこから蔵本モデルを表す式が登場。力学系で何をやるかというのを説明するため、パラメータをどう設定すれば振る舞いがかわるのか？みたいなものを2次元の蔵本モデル(考える振動子の状態が2つ)を使って説明。 2次元だと式変形で一次元の常微分方程式の問題に帰着できて、、、そこからt->∞とするとどうなるみたいな議論を展開してました。ここから3次元4次元と次元を増やした場合の解析はものすごく難しくなる、というところで下手に多次元のものを考えないで「Order Parameter」と呼ばれるものを考えて問題をシンプルにしていきました。このシンプルにした状態で、無限個あったときにどうなるかを次行こう考えて行きました。

2. 連続な蔵本モデル

振動子の数が無限、かつ連続的に存在すると仮定すると密度関数などを使って偏微分方程式の形で蔵本モデルの連続版は記述することができます。

f:id:maestro_L_jp:20171002003350j:plain

偏微分方程式の攻略法の一つとして、Fourier変換がありますが、今回もそれを使って「常微分方程式化」をして行きます。式変形を繰り返していく中で「無限次元版常微分方程式」の形に持って行きました。持っていく途中でnon linearの項を無視していましたが、これはどうも力学系的な安定性を調べる上では無視しても問題ないっぽい。間違っていたらごめんなさい。結局、この形の蔵本モデルをとくことに帰着します。

$\begin{cases} \frac{dZ_{1}}{dt} = (i\omega + \frac{K}{2} P) Z_{1} \\ \frac{dZ_{k}}{dt} = iK \omega Z_{k} \quad \quad\quad (k = 2, 3, …) \end{cases}$

この問題をとくためにスペクトル半群の考え方を用います。

3. 線形作用素のスペクトルと半群[一般論]

ここからは一般論の話。線形作用素の定義、関数解析の基本的な定理などの紹介はほぼほぼ割愛して、いきなりレゾルベント集合、スペクトルの定義に行きました。この辺りはこの数学カフェよりも前に行われた予習会でやっているだろうということで。。。半群関連で有名な定理として「Hille-Yoshidaの定理」が紹介されましたがそれの詳細な紹介も予習会でやっただろ、的なノリでこれも割愛。角域作用素については初めて定義を知りました。(一応connpassにのっていた文献にもそれの定義ありましたけどね。。)これは非有界作用素の性質のなかでも美味しい条件の一つで、今回のようなHille-Yoshidaの定理を使う半群にとってはわかりやすいものだったりします(間違っていたらごめんなさい。) あ、ちなみに連続線形作用素は角域作用素です。(この部分を証明したい人向けに角域作用素の定義を以下に記載します。)
定義

Banach空間 X 上で稠密に定義された閉作用素 $A$ とする。

$A$ : 角域作用素である <=> $\exists a ∈ R, 0 \lt \exists \phi \lt \pi / 2 \quad s.t. \quad \sigma (A) \subset S_{\phi, a}$

ここで、 $S_{\phi, a} \equiv \{ \lambda ∈ C \mid \pi - \phi \lt \arg |\lambda - a| \lt \pi + \phi \}$ とする。

個人的な所感ですが、この辺りで半群の生成作用素のスペクトルが全て負だとわかりやすい式でかけて振る舞いが調べやすいんだなと悟りました。

4. スペクトルと半群の理論を連続な蔵本モデルに適用

ここでは、作用素「 $T = i \omega + \frac{k}{2} P$ 」のスペクトルを調べることで蔵本モデルの安定性を議論しよう、というトピック。この作用素に対する固有方程式を考えていくと、この作用素の固有値は複素平面の正の実軸上にしか所属しない、ということがわかります。また、連続スペクトルは $\frac{k}{2} P$ がコンパクト作用素であることから $\sigma _{c} (T) = iR$ (複素平面でいう虚軸)に属することがわかります。(*) 固有方程式を発展させて計算していけばわかることみたいなのですが、 $K_{c} \lt K$ のときは自明解は不安定で有ることがわかる。これは同期現象的には「時間が経てば同期する」ということを意味している。しかし、 $0 \lt K \lt K_{c}$ のときは普通の理論ではわからないのでどうしよう？というので登場するのが一般化スペクトル理論。(なぜならKがこの値の範囲に入る時固有値は負の実軸の中に潜んでしまい、虚軸上にある連続スペクトルのせいでその固有値をとらえた議論ができなくなる(ラプラス変換の知恵が使えなくなる)からである。)

ここまで話を聞く限り、スペクトル理論が力学系の解の安定性を議論するのにものすごく使えるなーというのがわかりました。個人的には最初の(*)の部分の命題が非自明だったのでちょっと証明を考えてみようかと思っています。。。。しかし、数日考えたが証明が思い浮かばず。。

http://www.ne.jp/asahi/music/marinkyo/matematiko/kato.html.ja

のテキストに頼るしかないのか。。。

5. 一般化スペクトル理論[一般論]

一般化スペクトル理論の発想は、レゾルベントを有る意味でSchwarz超関数的な発想で「ある特殊なクラスの線形汎関数へ作用するもの」というふうに取り扱うということ。印象的だったのは扱う関数のクラスをL2から連続関数、さらに正則関数にまで落とし込んで考えていたのが印象的。正則関数まで落とし込んであげると解析接続を使って右半分から左半分(の一部)を使ってスペクトル理論を展開できるので先ほどの議論でとらえることのできなかった固有値を使った安定性理論を議論することができる、ということ。

あとで見つけたのですが、このテキストに一般化スペクトル理論について載っていますね。。。 http://www.ne.jp/asahi/music/marinkyo/matematiko/kato.html.ja

Gelfandの三つ組、一般化スペクトル、一般化レゾルベント、一般化固有値と定義とそのアイデアをバシバシ紹介していっていました。定義の仕方がかなり違うが結果がHilbert空間上のスペクトル理論と同じような結果が出ているのに面白みを感じます。ちなみに余談として「Barreled sp」という用語が出てきましたが、定義はこの中に貼っておきます。

樽型空間 - Wikipedia

6. 一般化スペクトル理論の蔵本モデルへの応用

一般化スペクトル理論を使って $0 \lt K \lt K_{c}$ のときの解析をしていきます。結果としては自明解は安定。つまり、Kがこの範囲にいるときは、同期することはない、ということです。さらっと紹介しちゃいましたが、実際の証明は計算のオンパレードみたいです。。。

7. 分岐

力学系には分岐理論というものもありまして、それの中心となる概念が「中心多様体・中心部分空間」と呼ばれるものです。ここの部分は私もしっかり理解はできていないのですが、蔵本モデルの場合だと $K_{c}$ 近傍で解の振る舞いがどう変わるかを調べていく、ということをやっていました。

8. 最近の研究紹介

この蔵本モデル、お互いに干渉し合う度合いは一様という条件がつきますが、現実はそういうケースはまれ。繋がりはグラフのエッジの重みで決まることがままある、ということでグラフと蔵本モデルをドッキングさせた理論について紹介。そして、この理論における最近の研究結果を紹介していただきました。ということでここまででおしまい。

一緒に出席していた友人曰く「なんで数学者はすぐに無限次元に拡張したがるんだろう？コンピュータではもう有限しか扱えないのに」とのことでした。これに関しては僕はフォローしようとしましたが、完全にしっくり来ていただいたかは謎。確かにコンピュータを使ってシミュレーションする場合とか実際問題は馬鹿でかい次元の有限次元なので。。。。無限の美味しい性質がまんまつかえるかはちょっと謎ですね。。でも、こういう無限次元について考えることは有限次元に近似していく上でもものすごく大事なことなので無限次元について考えるのは意味があることなのでは！と僕は信じています(だって微分ですら実際は離散化してコンピュータに計算させていますよね？現在こういうコンピュータ技術が発展していてもやはり微分について学ばなくていいということはないですよね。むしろ学んだ方がいい結果出るのはもう経験則でわかるのではと思います。)

まとめと感想

予習会に2度ほどお世話になったのと千葉先生の話し方がものすごくうまかったので大枠は理解した気になれました！そもそも作用素論を微分方程式の解析にどのように役立てているかの一旦が垣間みえて大変勉強になりました。あと、一般化スペクトル理論というものも知ることができたのはでかいです。これは自分が学生時代(作用素環論やってたんですが、この理論知らなかった…)では知らなかったのでね。これ自分である程度数学的に理解できるぐらい穴埋めやってみたら力尽きそうだなー。というか蔵本モデルを応用したプログラミングとかやったらどうなるんだろうなー。とか思ったり。今度作ってみようかなぁ。Androidアプリとか。

2017-07-24

【第20回数学カフェ】トロピカル幾何学に参加してきました。

7/23 (日)に【第20回数学カフェ】トロピカル幾何学に参加してきました。

connpass.com

会場はNTTデータ数理システム。実は私、この会社に何年か前に新卒として入社して数年ほどお世話になったことがあります(そのときはNTTデータ傘下ではなく、場所も信濃町ではなかったですが) 会場入りすると前に比べて断然広いセミナールームに驚きを隠せませんでした。

会場についての感想についてはここまでにして早速セミナーの中身についてのまとめに行きます。

今回の講師は東大数理の植田先生。

1. 代数幾何について

いきなりトロピカル半環の定義…と行かずにまずは代数幾何の初歩的な定義から。多項式環の零点集合を代数多様体と定義して…というところから。いきなりトロピカル半環の定義から入るとモチベーションがちょっと下がっちゃうからだろうか。事前に

http://www.math.sci.hokudai.ac.jp/~ishikawa/tropical/ishikawa-tropical07.pdf

とかのぞいていたのですが、これだけだと背景は分かり辛いですね。。。

副次的なメリットとして代数多様体についての議論についていい復習になったということでしょうか。 (が、脱線がすごく、しかも脱線した時の話の中身がもう大学院のセミプロしかわからないようなものばかりでしたよ…?)

この代数多様体の話がだいたい全講義の３分の2の時間を費やしましたね。。

あと、ここでちょっと面白いと思った定理は「任意の有限生成k代数はあるk多項式の剰余環と同型である」というHilbertの定理。これまで数学では構造的に証明されてたものが初めて論理だけ(非構造的だけど)で証明したとかなんとか。

2. トロピカル半環とアメーバについて

トロピカル半環の例と零点集合の定義と例、アメーバの定理について話されました。トロピカル幾何においては+をmaxで定義してもminで定義しても本質的には変わらないんだという感じでした。 …が私の数学力がないせいか、ここから先は十分な感想を書けずじまい。。。

その後…

結局、半分以上脱線していたがなかなか面白かったです。ただ、このトロピカル半環(およびトロピカル幾何)は実社会、応用数理ではどう役に立つのかは知りたかったですね。でも、この辺ってまだ応用には未開拓なんでしょうか。トロピカル代数自体はルート検索のアルゴリズムでよく知られているワーシャル-フロイド法の数学的定式化にも使われているとか。

proc-cpuinfo.fixstars.com

その後、懇親会にも参加。ペルー料理を堪能しました。そこで岩沢理論についての話と数理物理についての話をちらっとさせていただきました。

まとめと所感

トロピカル半環自体は定義は難しくないのですが、背景とかトロピカル幾何になってくるとだいぶ難しさ度合いが変わってくるなという印象でした。このトロピカルという考え方は実社会で活かせるのだろうか？というのもちょっと考えてみたりしています。。。