数学カフェ Advent Calendar 12/11分の記事です。
1. はじめに
みなさま、こんばんは。まえすとろ(@maestro_L_jp)です! 僕は学生の頃数学科で数学の勉強をしていました。その中で大学院では作用素環論を専攻していました。作用素環論は「Hilbert空間上の有界線型作用素たちから構成される環の構造について調べる理論」です。この分野について勉強するために関数解析の必須の知識となります。なので、ある程度の知識は有していたりします。 そして、数学カフェで何回かに渡り、関数解析の予習会+復習会が開催され私もそのうち何回か参加させていただきました。そこでCompact作用素とFredholm作用素についてのトピックを扱っていたので、これを使った題材で書こう!と思った次第です。 とはいえ、今は(昔からだったかもですが)最先端の内容を話すことできないので、Compact作用素、Fredholm作用素の議論を、掛け算作用素でやったらどうなるか、ということについて書いていこうかと思います。自分はこの掛け算作用素に帰着して一般的な作用素の議論を理解してきました。関数解析で作用素論とか勉強する人にとって中身をしっかり味わうための触媒的なものになれば幸いです。
ここから口調が数学のテキストっぽくなります。 あと、第3章以降の命題・定理の証明は以下のpdfファイルにまとめてあります。ちょっと乱調気味ですがご了承ください。 https://drive.google.com/open?id=1mVHh0MzljqHZdNq7Nz2Iq2WWt5SFqJOO
なお、今回は話を簡単にするためBanach空間でなく同一のHilbert空間上の線型作用素に限定してお話しさせていただきます。
2. 今回取り扱う概念の定義と命題・定理
Def 2.1.
Hilbert空間 から
への線型作用素
が以下の条件を満たす時、
は有界である(有界線型作用素 or 連続線型作用素)と定義する。
$$ {}^\exists M > 0 \ \ \ s.t. \ \ \ {}^\forall x \in \mathscr{H} \ \ \ \Vert Tx \Vert \leq \Vert x \Vert $$
このとき、のノルムを
と定める。
また、
から
への線型作用素を
上の線型作用素
という。
Prop 2.2. Hilbert空間 から
への線型作用素
について以下は同値。
(1) は有界である。
(2) が
の収束列ならば、
は
の収束列で、
が成り立つ。
(ただし、 。)
Def 2.3. Hilbert空間 から
への線型作用素
が以下の条件を満たすとき、
はCompact作用素である(あるいは完全連続線型作用素)と定義する。
Prop 2.4. Compact作用素は有界線型作用素である。
Def 2.5. Hilbert空間 上の有界線型作用素
について、以下の条件を満たす有界線型作用素
を
の共役作用素という。
$$ \langle T^* x, y \rangle = \langle x, Ty \rangle \ \ ( {}^\forall x, y \in \mathscr{H})$$
特に、が成り立つ時、
を自己共役作用素という。
Prop 2.6. 有界線型作用素に対する共役作用素
は一意に存在する。
Def 2.7. Hilbert空間 上の有界線型作用素
が以下の3つの条件を満たす時、
はFredholm作用素であると定義する。
(1) は有限次元。
(2) は有限次元。
(3) は
の閉部分空間。
Prop 2.8. 有界線型作用素がFredholm作用素である必要十分条件は、
$$ ST = I - K, \ \ \ TS' = I - K'$$
となる有界線型作用素とCompact作用素
が存在することである。(ただし、
は恒等作用素である。以後、
は恒等作用素とする)
Def 2.9.
(1) 複素数が有界線型作用素
についてが可逆な有界線型作用素を持つ時、
は有界線型作用素
のレゾルベントという。
のレゾルベント全体の集合を
と書く。
(2) を
のスペクトル集合といい
と書く。
の元を
のスペクトルという。
(3) のスペクトル
について、
となる非ゼロのベクトル
が存在する時、この
を点スペクトル(いわゆる固有値)といい、点スペクトル全体の集合を
と書く。
をスペクトル
に対する固有空間という。
(4) のスペクトル
について、
は単射かつ
は
の中で稠密だが、
は有界でない場合、この
を連続スペクトルといい、連続スペクトル全体の集合を
と書く。
Thm 2.10. (Fredholm Alternative)
Compact作用素 について以下のどちらかが必ず成り立つ。
Prop 2.11. (Compact作用素のスペクトル)
・Compact作用素のスペクトル集合は0以外の集積点を持たない。
・Compact作用素のスペクトルについて、
の固有空間は有限次元。
Def 2.12.
複素数が有界線型作用素
について、
がFredholm作用素にならない時、
は有界線型作用素
の本質的スペクトルといい、本質的スペクトル全体の集合を
と書く。
有界線型作用素はどんなものかはイメージしやすいが、Compact作用素やFredholm作用素、上記の命題・定理などは初学者にとってはイメージしづらいものである。次の章で「数列空間上の掛け算作用素」をベースにした議論を行い本章で紹介した定義・命題・定理などを理解しやすい形に昇華していく。
3. 掛け算作用素についての基本的な性質
以下、Hilbert空間として複素数列空間 を取り扱う。
Prop 3.1.
を
上に属する複素数列とする。
線型作用素を
$$ M_c x := \lbrace c_n x_n \rbrace_n \ \ \ \ ( x \in l^{2})$$
このを掛け算作用素という。
以下、掛け算作用素の基本的な性質を紹介する。
について、以下が成り立つ。
(1)
(2)
(3)
について、
の共役作用素は
である。
ただし、
である。
Prop 3.4. 掛け算作用素が自己共役作用素であるための必要十分条件は
が実数列であることである。
4. 掛け算作用素上でのCompact作用素・Fredholm作用素の理論
まず、掛け算作用素がCompact作用素になる条件を条件を与える。これをベースにCompact作用素、Fredholm作用素にまつわる諸定理との関連を述べる。
Prop. 4.1.
掛け算作用素がCompact作用素になる必要十分条件は
が0に収束する数列になることである。
この命題から言えることは、Compact掛け算作用素を取り扱う際、0に収束する数列をイメージしていけばOKということになる。(ここから得られた知見は、掛け算作用とは限らないCompact作用素について取り扱う時の道しるべになったりする)
数列は横軸にindex, 縦軸に項の値をとる座標を考えると、実数列の絶対値は図にプロットできる(図1)。

これだけでも数列の振る舞いはわかる。プロットした点を結ぶようにグラフを書くと、nを十分大きくしていったときの振る舞いがわかりやすくなる(図2)。
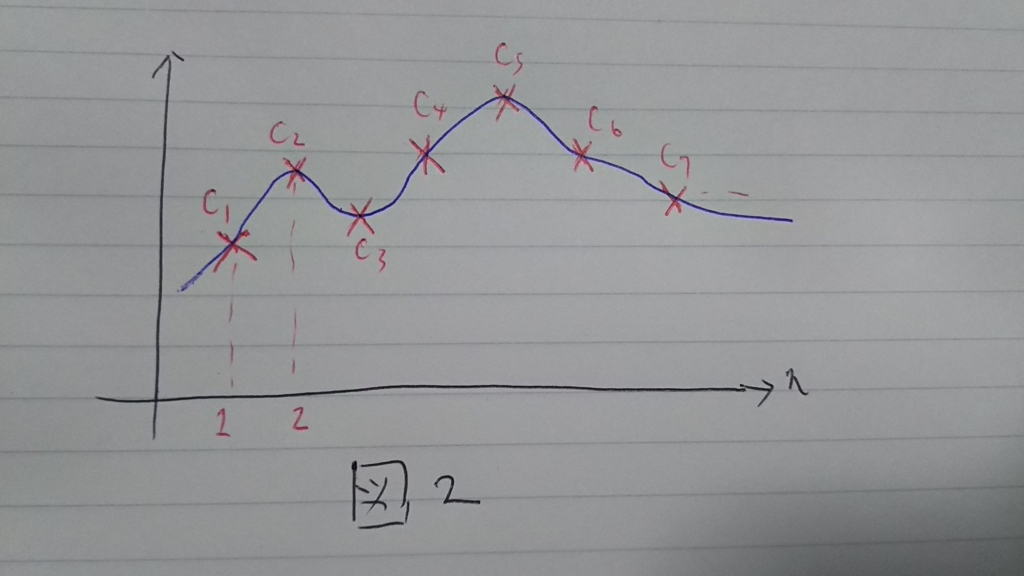
Compact自己共役掛け算作用素に対応する収束列
は以下のように図示できる(図3)。
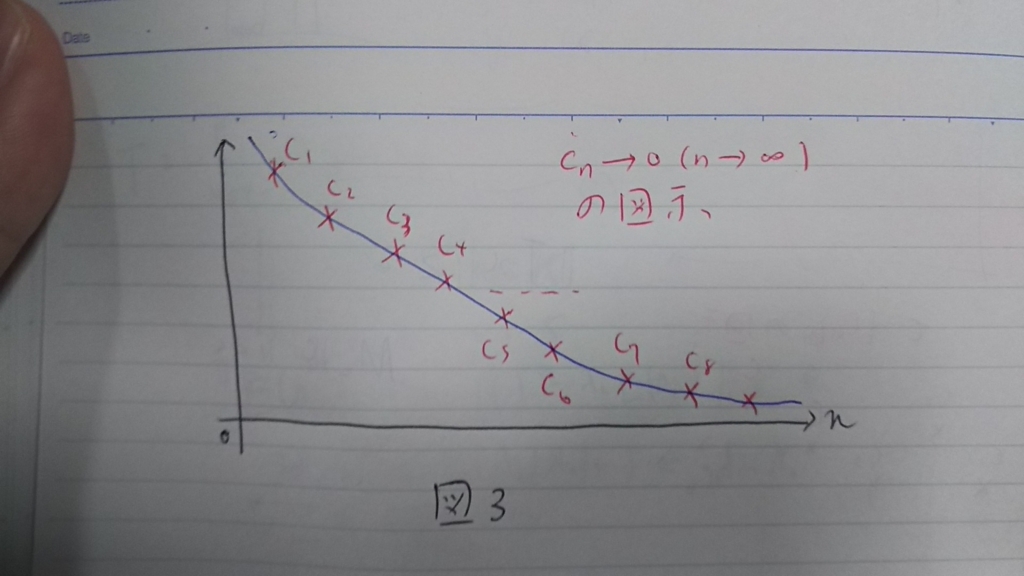
ここで、作用素を考える。この作用素は掛け算作用素になり対応する数列
は
となる。
がCompact作用素なら、
は0への収束になるので、
は1への収束列になる。図4に
を図示したものを表示させる。

この図から見えてくるのは、「nが十分大きくした場合、数列の値は「1」との距離が0.5以下になる」ということである。が可逆かどうかはindexが若い有限個の項だけみていいだろうとあたりがつく。このことは以下に定理としてあげる。
Thm 4.2. (掛け算作用素版Fredholm Alternative)
Compact掛け算作用素 について以下のどちらかが必ず成り立つ。
掛け算作用素がFredholm作用素になる条件を条件を与える
Prop.4.3. 掛け算作用素がFredholm作用素である必要十分条件は、以下の2つを満たすことである。
(1) 対応する数列の集積点に0を含まないことである。
(2) 対応する数列の中で0に値をとる項は高々有限個。
自己共役掛け算作用素に対応する数列について以下に図示する。Fredholm作用素である例とそうでないものの例を図示する(図5)。
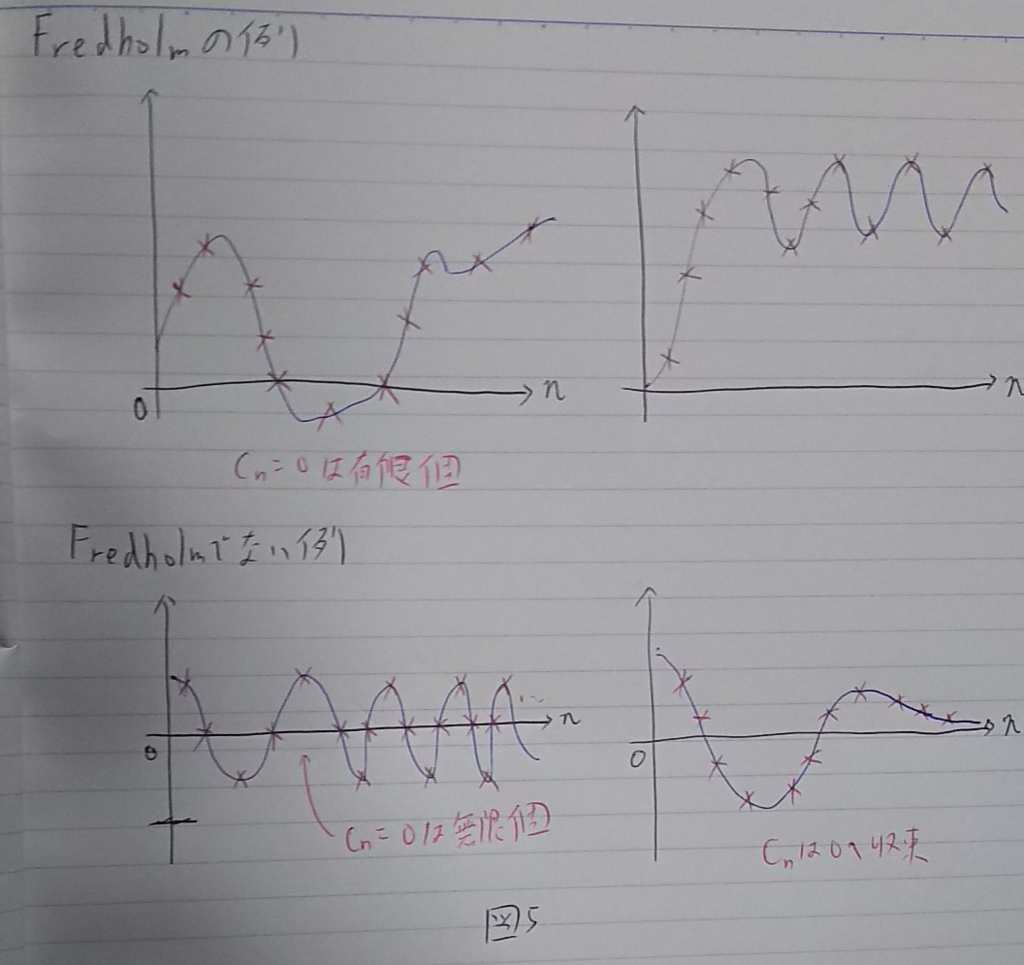
以下の命題はProp 2.8. の掛け算作用素版である。別資料に証明は記載するが、Fredholm掛け算作用素の場合は、点列ベースで考えていけば直感から外れることなく、かつ数学的に厳密な方法で証明できる。
Prop 4.4. 掛け算作用素がFredholm作用素である必要十分条件は、
$$ M_d M_c = I - M_k, \ \ \ M_c M_{d'} = I - M_{k'}$$
となると0への収束列
が存在することである。
掛け算作用素のスペクトルについても議論する。
Prop 4.5.
掛け算作用素のスペクトルについて以下が成り立つ。
が成り立つ。(補足するとは数列のとる値の集積点の中で、実際に値を取る項が存在しない。)
Ex 4.6.
数列 に対応する掛け算作用素
については
となる。以下に数列 について図示する。以下の図で点スペクトルが実際数列の項がとる値、連続スペクトルが収束先になることも図示する(図7)。

これは掛け算作用素のスペクトルについて調べるには数列のとる値を調べていけばいいということを主張している。
掛け算作用素については以下のことも言える。
Prop 4.7. 掛け算作用素におけるスペクトルの固有空間の次元はその値をとる数列の項の数である。
この事実とCompact掛け算作用素が0への収束列に対応することから、以下の定理が成り立つ。
Thm 4.8. (Compact掛け算作用素のスペクトルと固有空間)
・Compact掛け算作用素のスペクトル集合は0以外の集積点を持たない。
・Compact掛け算作用素のスペクトルについて、
の固有空間は有限次元。
Prop 4.9. (掛け算作用素の本質的スペクトル)
掛け算作用素の本質的スペクトルについて以下が成り立つ。
自己共役掛け算作用素に対応する実数列
を図示して本質的スペクトルがどういうものかイメージしやすいようにしておく(図8)。
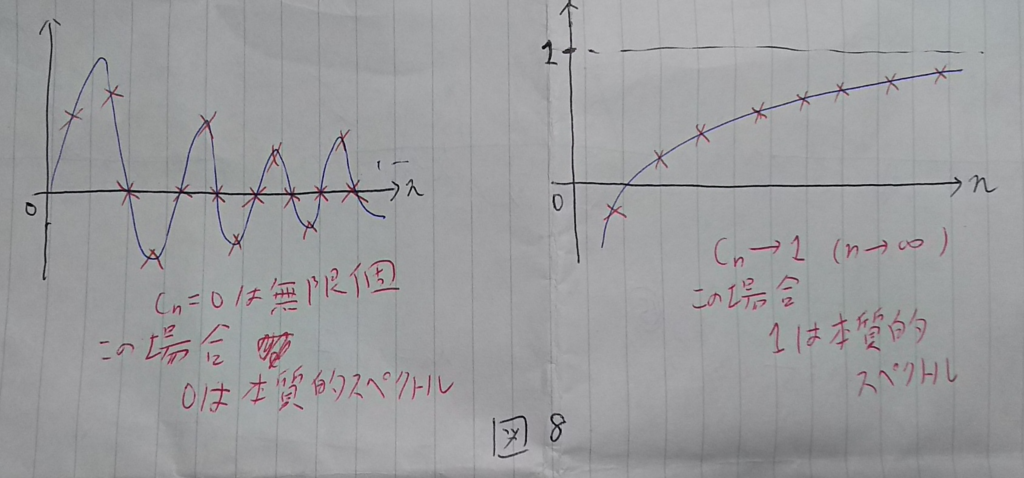
5. まとめ
いかがだったでしょうか。掛け算作用素ベースでCompact作用素やFredholm作用素を扱うと意外と敷居が低くイメージしやすいと思います。この帰着によって私は作用素論の理解を深めていきました(ただし、万人にこの方法で以下はまた別問題…)
特に一番このイメージが効いたのは以下の定理の証明を読み解いていくときである。(というか、修論もこのイメージがなければ書けなかった。。)
(1)
(2) 等式 を満たすユニタリー作用素
とCompact作用素
が存在する。
この定理はWyle - von Neumann の定理の応用として、次のAdvent Calenderで証明していきます。